Teorema de Pitágoras

Si el triángulo tiene un ángulo recto (90°)... y pones un cuadrado sobre cada uno de sus lados, entonces... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos! El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
a² + b² = c²
Historia[editar]
Respecto de los babilonios hay esta nota:
Desde el punto de vista matemático, las novedades más importantes que registran los textos babilónicos re refieren a la solución algebraica de ecuaciones lineales y cuadráticas, y el conocimiento del llamado "teorema de Pitágoras" y de sus consecuencias numéricas.
El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la mística escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación [cita requerida]. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
Designaciones convencionales[editar]
| Vértices |  |  |  |
| Lados (como segmento) |  |  |  |
| Lados (como longitud) |  |  |  |
| Ángulos |  |  |  |
Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se formula que:
, se formula que:
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se formula que:
, se formula que:(1)
De la ecuación () se deducen fácilmente tres corolarios de verificación algebraica y aplicación práctica:
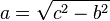 |  | 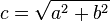 |
Ejemplos:
Números Racionales
Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones. Todos los números fraccionarios son números racionales, y sirven para representar medidas. Pues a veces es más conveniente expresar un número de esta manera que convertirlo a decimal exacto o periódico, debido a la gran cantidad de decimales que se podrían obtener.
Los números racionales limitados: cuya representación decimal tiene un número determinado y fijo de cifras, por ejemplo 1/8 es igual a 0,125.
Los números racionales periódicos: A su vez los números racionales periódicos se dividen en dos, los periódicos puros, cuyo patrón se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363… y los periódicos mixtos, de los cuales el patrón se encuentra después de un número determinado de cifras, por ejemplo 5,48176363636363…
Los números racionales limitados: cuya representación decimal tiene un número determinado y fijo de cifras, por ejemplo 1/8 es igual a 0,125.
Los números racionales periódicos: A su vez los números racionales periódicos se dividen en dos, los periódicos puros, cuyo patrón se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363… y los periódicos mixtos, de los cuales el patrón se encuentra después de un número determinado de cifras, por ejemplo 5,48176363636363…
Propiedades de los números racionales
Existen para la suma y resta, y para la multiplicación y división, distintas propiedades de los números racionales, estos son:
Entre las propiedades de la suma y resta están:
-Propiedad interna: según la cual al sumar dos números racionales, el resultado siempre será otro número racional, aunque este resultado puede ser reducido a su mínima expresión si el caso lo necesitara.
Ejemplo:

-Propiedad asociativa: se dice que si se agrupa los diferentes sumandos racionales, el resultado no cambia y seguirá siendo un número racional. Veamos:
Ejemplo:
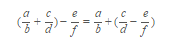
Propiedad conmutativa: donde en la operación, si el orden de los sumando varía, el resultado no cambia, de esta manera:
Ejemplo:

-Elemento neutro: el elemento neutro, es una cifra nula la cual si es sumada a cualquier número racional, la respuesta será el mismo número racional.
Ejemplo:

-Inverso aditivo o elemento opuesto: es la propiedad de números racionales según la cual, existe un elemento negativo que anula la existencia del otro. Es decir que al sumarlos, se obtiene como resultado el cero.
Ejemplo:

Por otro lado, existen también las propiedades de los números racionales por parte de la multiplicación y la división, y estas son:
-Propiedad interna: en razón de que al multiplicar números racionales, el resultado también es un número racional.
Ejemplo:

Esta además se aplica con divición:

-Propiedad asociativa: donde al agrupar diferentes factores la forma de la agrupación, no altera el producto.
-Propiedad conmutativa: aquí se aplica la famosa frase, el orden de los factores no altera el producto, entre los números racionales también funciona.
Propiedad distributiva.- al combinar sumas y multiplicaciones, el resultado es igual a la suma de los factores multiplicado por cada uno de los sumandos.
-Elemento neutro en la multiplicación y la división de números racionales: existe un elemento neutro que es el número uno, cuyo producto o cociente con otro número racional, dará como resultado el mismo número.
Ejemplos de números racionales
Los números racionales son números fraccionarios, es decir que podríamos escribir cualquier
cociente entre dos números enteros y llamarlo número racional.
Aunque también podría ser expresado de esta manera: 5/7
Sin embargo, los números enteros también pueden ser incluidos dentro de los números Q, al formar un cociente con un número neutro, es decir de este modo:
Aunque también podríamos expresar el número entero 3, en forma de fracción, en el caso de necesitarlo en alguna operación matemática, pues al simplificarlo obtenemos la misma respuesta:






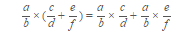





Mardito ladron
ResponderEliminar